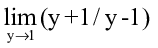Differential Calculus
1) The luminous intensity I candelas of a lamp at varying voltage V is given by: I = 4 × 10⁻⁴ V². Determine the voltage at which the light is increasing at a rate of 0.6 candelas per volt.
- 750
- 450
- 550
- 650
Answer: 750
2) The length l meters of a certain metal rod at temperature θ°C is given by l = 1 + 0.00005θ + 0.0000004θ². Determine the rate of change of length in mm/°C when the temperature is 100°C.
- 0.43
- 0.33
- 0.13
- 0.23
Answer: 0.13
3) The distance x meters described by a car in time t seconds is given by: x = 3t³ − 2t² + 4t − 1. Determine the acceleration when t = 0.
- 7
- -4
- -7
- 4
Answer: -4
4) Supplies are dropped from a helicopter and distance fallen in time t seconds is given by x = 1/2gt² where g = 9.8 m/sec². Determine the velocity and acceleration of the supplies after it has fallen for 2 seconds.
- v = 19.6 m/sec, a = 9.8 m/sec²
- v = 9.8 m/sec, a = 19.6 m/sec²
- v = 18.6 m/sec, a = 8.8 m/sec²
- v = 19 m/sec, a = 10 m/sec²
Answer: v = 19.6 m/sec, a = 9.8 m/sec²
5) A boy, who is standing on a pole of height 14.7m throws a stone vertically upwards. It moves in a vertical line slightly away from the pole and falls on the ground. Its equation of motion in meters and seconds is x = 9.8 t − 4.9t². Find the time taken for downward motions.
- 3
- 2
- 5
- 4
Answer: 2
6) A ladder 10m long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1m/sec, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6m from the wall?
- 3/4
- 2/3
- 1/3
- 1/7
Answer: 3/4
7) A car A is travelling from west at 50 km/hr. and car B is travelling towards north at 60 km/hr. Both are headed for the intersection of the two roads. At what rate are the cars approaching each other when car A is 0.3 kilometers and car B is 0.4 kilometers from the intersection?
- 86
- 78
- 77
- 95
Answer: 78
8) A water tank has the shape of an inverted circular cone with base radius 2 metres and height 4 metres. If water is being pumped into the tank at a rate of 2m³/min, find the rate at which the water level is rising when the water is 3 m deep.
- 8/9π
- 6/5π
- 1/9π
- 8/7π
Answer: 8/9π
9) Find the equations of the tangent to the curve y = x³ at the point (1,1)
- y = 3x – 1
- y = 3x + 1
- y = 3x + 2
- y = 3x – 2
Answer: y = 3x – 2
10) Determine
- 11
- 17
- 10
- 15
Answer: 10
11) Determine
- 6
- 5
- 4
- 3
Answer: 6
12) Determine
- 35
- 20
- 45
- 25
Answer: 20
13) Determine
- 0
- 3
- 9
- 1
Answer: 0
14) Determine
- 3
- 9
- 4
- 5
Answer: 3
15) Determine
- 2
- 4
- 3
- 1
Answer: 4
16) Determine
- 4
- 6
- 5
- 7
Answer: 7
17) Determine
- 52/6
- 57/6
- 37/6
- 32/6
Answer: 37/6
18) Determine
- Not defined
- -1
- 0
- 1
Answer: Not defined
19) Determine
- 1
- Does not exist
- 0
- 6
Answer: Does not exist
20) Determine
- 3
- -3
- Not defined
- 0
Answer: 3
21) Determine
- 3
- 0
- Not defined
- -3
Answer: 3
22) Determine
- √7/6
- √3/6
- √8/9
- √5/6
Answer: √3/6
23) Given g(x) = 3x², determine the gradient of the curve at the point x = −1
- -6
- 6
- 4
- -8
Answer: -6
24) Given the function f(x) = 2x² − 5x, determine the gradient of the tangent to the curve at the point x = 2
- 3
- 6
- 8
- -8
Answer: 3
25) Determine the gradient of k(x) = −x³ + 2x + 1 at the point x = 1
- 3
- 6
- 5
- -1
Answer: -1
26) Given: f (x) = −x² + 7. Find the average gradient of function f, between x = −1 and x = 3
- 7
- -2
- 5
- 6
Answer: -2
27) Given: f (x) = −x² + 7, find the gradient of ‘f’ at the point x = 3
- -7x
- -8x
- -4x
- -2x
Answer: -2x
28) Determine the gradient of the tangent to g if g(x) = 3/x
- 6/a²
- 3/a²
- -3/a²
- -6/a²
Answer: -3/a²
29) Determine the equation of the tangent to H(x) = x² + 3x at x = −1
- y = x – 1
- y = -x – 1
- y = x +1
- y = - x +1
Answer: y = x – 1
30) Use the rules of differentiation to find the derivative of y = 3x⁵
- 5x⁴
- 15x⁴
- 3x⁴
- 12x⁴
Answer: 15x⁴